Author:
(1) Yitang Zhang.
Table of Links
- Abstract & Introduction
- Notation and outline of the proof
- The set Ψ1
- Zeros of L(s, ψ)L(s, χψ) in Ω
- Some analytic lemmas
- Approximate formula for L(s, ψ)
- Mean value formula I
- Evaluation of Ξ11
- Evaluation of Ξ12
- Proof of Proposition 2.4
- Proof of Proposition 2.6
- Evaluation of Ξ15
- Approximation to Ξ14
- Mean value formula II
- Evaluation of Φ1
- Evaluation of Φ2
- Evaluation of Φ3
- Proof of Proposition 2.5
Appendix A. Some Euler products
Appendix B. Some arithmetic sums
14. Mean-value formula II
Recall that we always assume ψ is a primitive character (mod p), p ∼ P. Sometimes we write pψ for the modulus p.
Let k ∗ = {κ ∗ (m)} and a ∗ = {a ∗ (n)} denote sequences of complex numbers satisfying
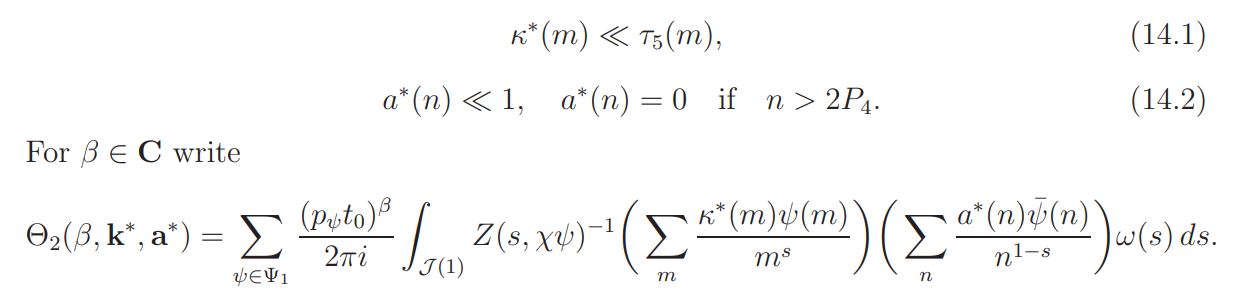
The goal of this section is to prove
Proposition 14.1. Suppose |β| < 5α. Then




This paper is available on arxiv under CC 4.0 license.

