Author:
(1) Attila Losonczi.
Table of Links
1.1 Basic notions and notations
1.2 Basic definitions from [7] and [8]
2 Generalized integral
2.1 Multiplication on [0, +∞) × [−∞, +∞]
2.3 The integral of functions taking values in [0, +∞) × [0, +∞)
2.2 Measurability
First we need to define measurability of generalized functions.
Definition 2.10. Let (K, S) be a measurable space (i.e. S is a σalgebra on P(K)). Let f : K → [0, +∞) × [0, +∞) be a function. We say that f is measurable if for each (d, m) ∈ [0, +∞) × [0, +∞) {x ∈ K : f(x) < (d, m)} ∈ S holds.
Proposition 2.11. Let (K, S) be a measurable space and f : K → [0, +∞) × [0, +∞). Then the following statements are equivalent.
-
f is measurable.
-
For each (d, m) ∈ [0, +∞) × [0, +∞], {x ∈ K : f(x) ≤ (d, m)} ∈ S.
-
For each (d, m) ∈ [0, +∞) × [0, +∞], {x ∈ K : (d, m) < f(x)} ∈ S.
-
For each (d, m) ∈ [0, +∞) × [0, +∞], {x ∈ K : (d, m) ≤ f(x)} ∈ S.
Proof. All equivalences simply follow from the fact that the space [0, +∞) × [0, +∞] is first countable and T2.
Proposition 2.12. Let (K, S) be a measurable space and f : K → [0, +∞) × [0, +∞) be measurable. Then the following statements hold.
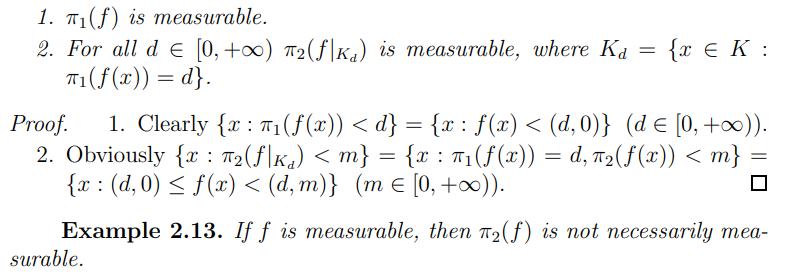
Let K = [0, 1], S be the Borel sets, g: [0, 1] → [0, 1] be a non Borel measurable function and f(x) = (x, g(x)) when x ∈ [0, 1]. Clearly {x ∈ K: f(x) < (d, m)} equals to either {x ∈ K: x < d} or {x ∈ K: x ≤ d}, and both sets are Borel, hence f is measurable.
Proposition 2.14. Let (K, S) be a measurable space and f: K → [0, +∞) × [0, +∞) be measurable and (d′, m′) ∈ [0, +∞)×[0, +∞). Then (d′, m′)f is measurable as well.
Proof. Let (d, m) ∈ [0, +∞) × [0, +∞).
If (d ′, m′) = (0, 0), then the statement is trivial.
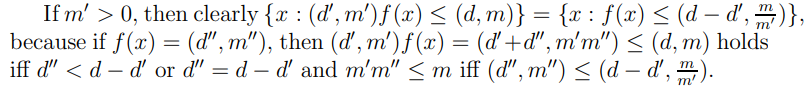
If m′ = 0, d′ > 0, then {x: (d′, m′)f(x) ≤ (d, m)} = {x: f(x) ≤ (d − d′, +∞)}, where similar argument works
Proposition 2.15. Let (K, S) be a measurable space and f, g : K → [0, +∞) × [0, +∞) be measurable. Then f + g is measurable as well.
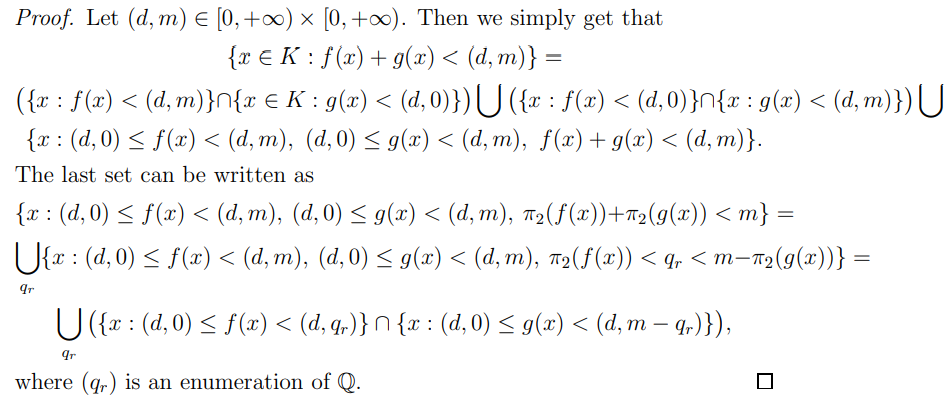
This paper is available on arxiv under CC BY-NC-ND 4.0 DEED license.

