Author:
(1) Yitang Zhang.
Table of Links
- Abstract & Introduction
- Notation and outline of the proof
- The set Ψ1
- Zeros of L(s, ψ)L(s, χψ) in Ω
- Some analytic lemmas
- Approximate formula for L(s, ψ)
- Mean value formula I
- Evaluation of Ξ11
- Evaluation of Ξ12
- Proof of Proposition 2.4
- Proof of Proposition 2.6
- Evaluation of Ξ15
- Approximation to Ξ14
- Mean value formula II
- Evaluation of Φ1
- Evaluation of Φ2
- Evaluation of Φ3
- Proof of Proposition 2.5
Appendix A. Some Euler products
Appendix B. Some arithmetic sums
Appendix A. Some Euler Products
This appendix is devoted to proving Lemma 8.3, 15.2, 15.3, 16.1 and 16.2. For notational simplicity we shall write
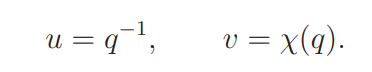
Proof of Lemma 8.3. Note that

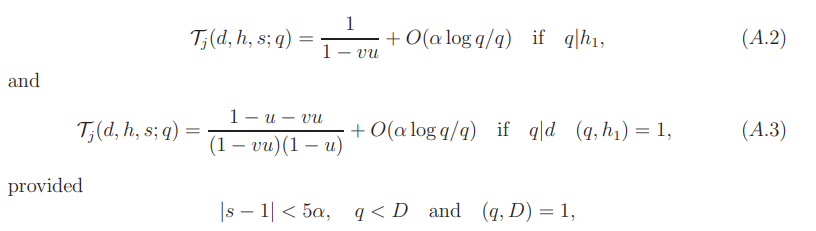
which are henceforth assumed. We discuss in three cases.
Case 1. (q, dh) = 1.
We have
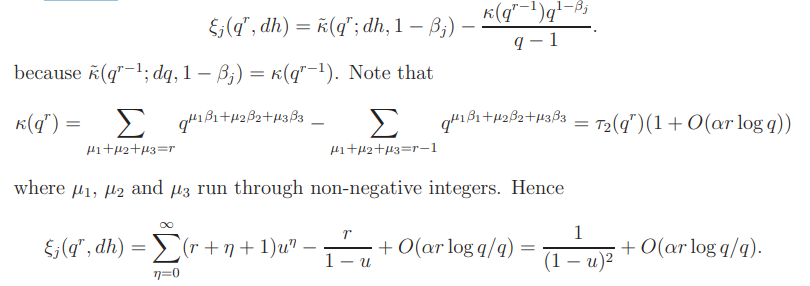
It follows that
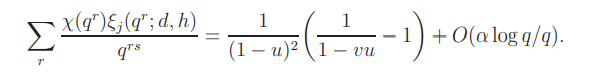
This together with the relations
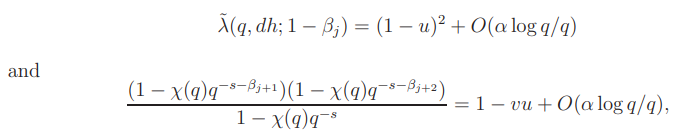
yields (A.1).
Case 2. q|h.
We have
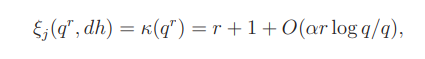
so that
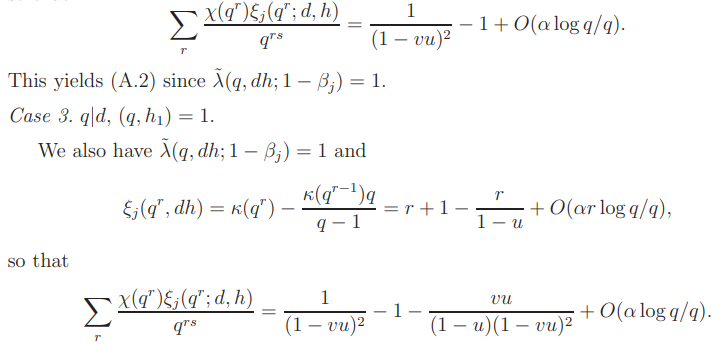
This yields (A.3).

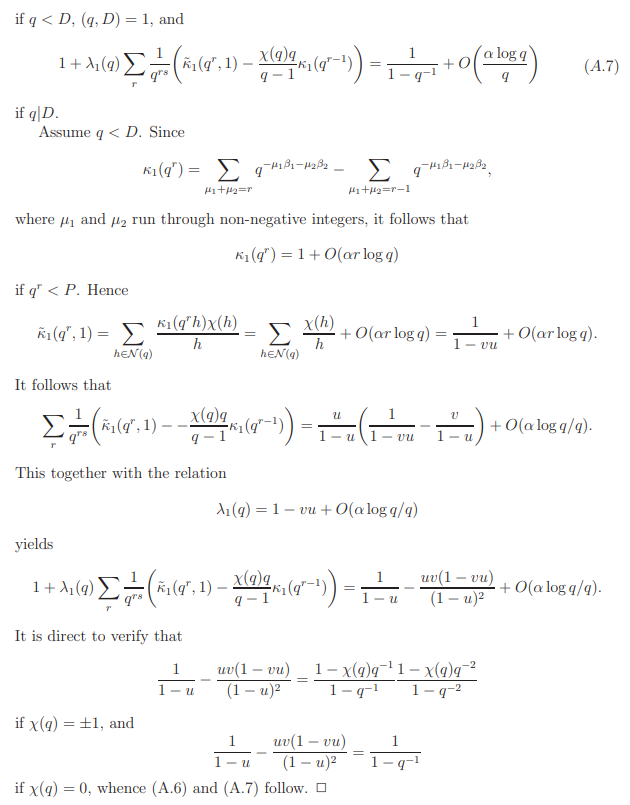

This completes the proof.
Proof of Lemma 16.1. For any q, r, d and l we have
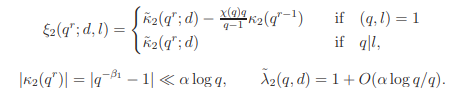
Hence
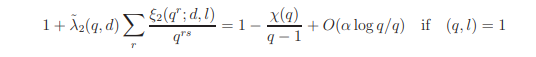
and
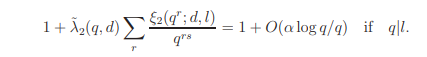
On the other hand we have
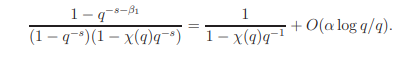
It follows that
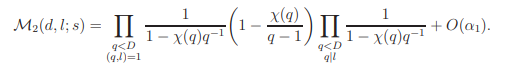
It is direct to verify that in either case the assertion holds.
Proof of Lemma 16.2. We give a sketch only. If dl < D, (dl, D) = 1 and |s − 1| ≤ 5α, then
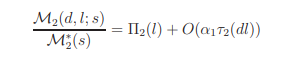
with
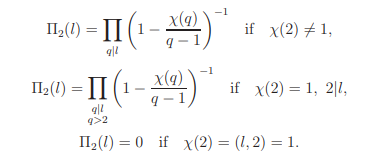
The assertion follows by discussing the cases χ(2) 6= 1 and χ(2) = 1 respectively
This paper is available on arxiv under CC 4.0 license.