Author:
(1) Yitang Zhang.
Table of Links
- Abstract & Introduction
- Notation and outline of the proof
- The set Ψ1
- Zeros of L(s, ψ)L(s, χψ) in Ω
- Some analytic lemmas
- Approximate formula for L(s, ψ)
- Mean value formula I
- Evaluation of Ξ11
- Evaluation of Ξ12
- Proof of Proposition 2.4
- Proof of Proposition 2.6
- Evaluation of Ξ15
- Approximation to Ξ14
- Mean value formula II
- Evaluation of Φ1
- Evaluation of Φ2
- Evaluation of Φ3
- Proof of Proposition 2.5
Appendix A. Some Euler products
Appendix B. Some arithmetic sums
6. Approximate formula for L(s, ψ)
Write
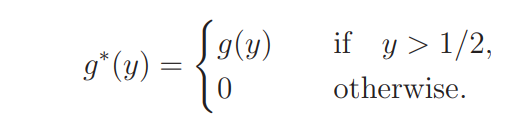
Let
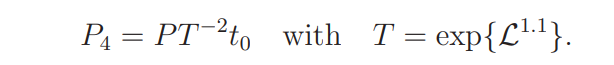
Lemma 6.1. Suppose ψ(mod p) ∈ Ψ, |σ − 1/2| < 2α and |t − 2πt0| < L1 + 2. Then
L(s, ψ) = K(s, ψ) + Z(s, ψ)N(1 − s, ψ¯) + O(E1(s, ψ)),
where
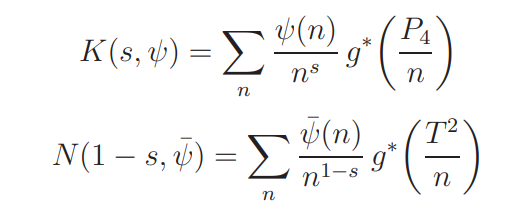
and where
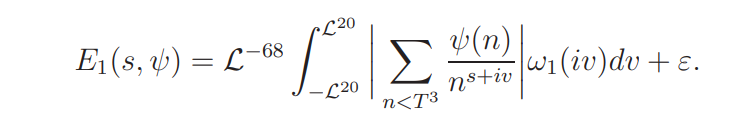
Proof. By (4.3) we have
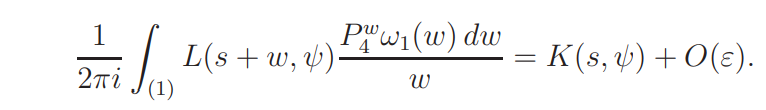
The left side above is, by moving the line of integration to u = −1, equal to
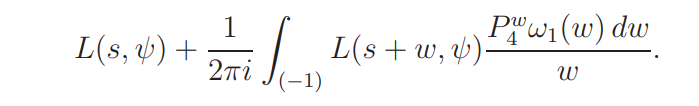
It therefore suffices to show that
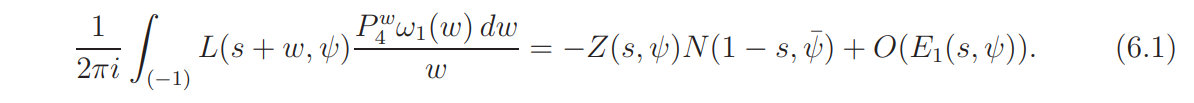
For u = −1 we have, by the functional equation (2.2) with θ = ψ,
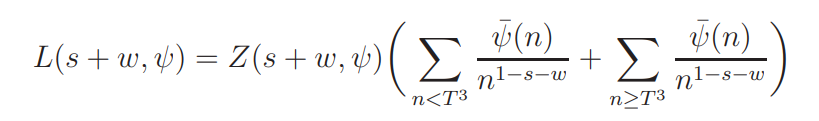
We first show that
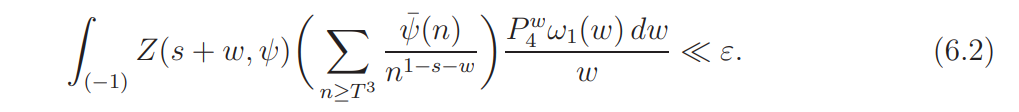
We move the contour of integration in (6.2) to the vertical segments
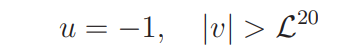
and
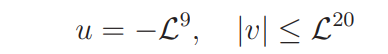
with the horizontal connecting segments
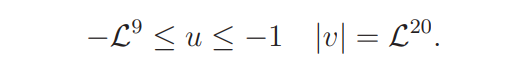

whence (6.2) follows. The proof of (6.1) is therefore reduced to showing that
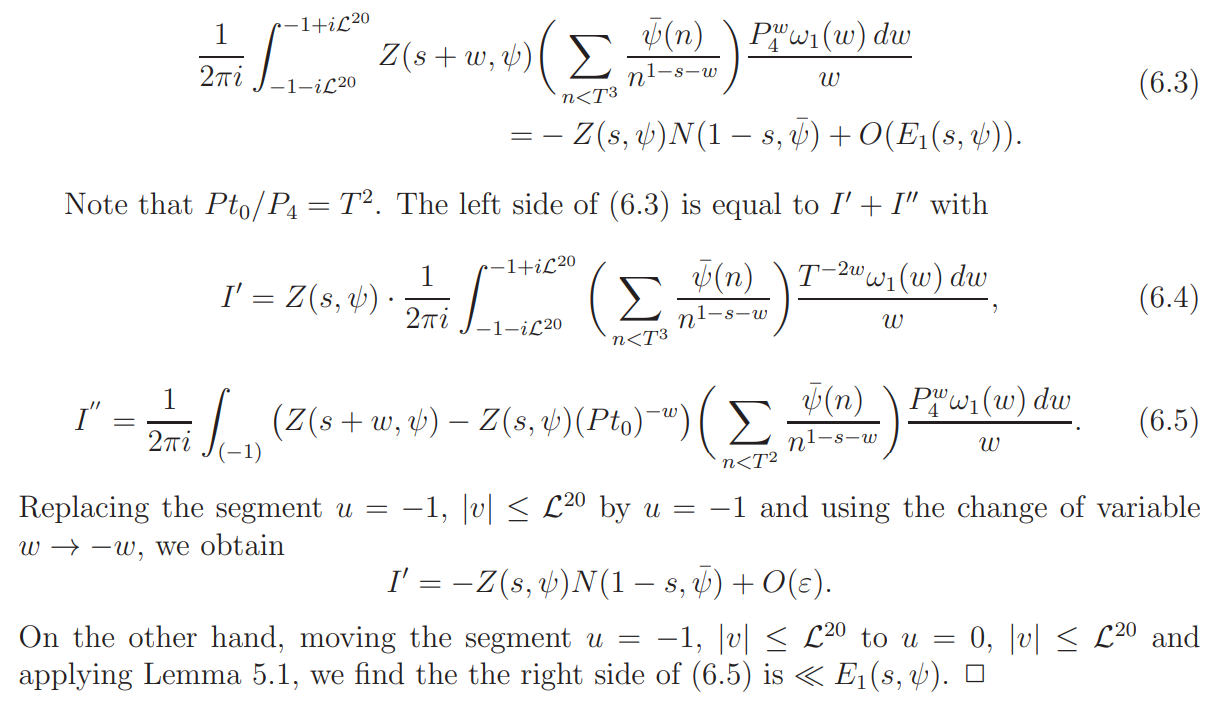
This paper is available on arxiv under CC 4.0 license.

